En las matemáticas se conoce el concepto de números racionales para hacer referencia a aquellos indicadores que permiten conocer el cociente entre dos números enteros. La noción de racional proviene de ración (parte de un todo). Los números racionales están formados por los números enteros (que pueden expresarse como cociente: 5= 5/1, 38=38/1) y los números fraccionarios (los números racionales no enteros: 2/5, 8/12, 69/253).
Cada uno de los números enteros posee otro carácter que le sigue; de tal modo que al -1 le sigue el 0 y a éste el 1, sucesivamente, y a su vez entre cada uno de éstos existen infinitos números no racionales.
Los números racionales permiten expresar medidas. Cuando se compara una cantidad con su unidad, se obtiene, por lo general, un resultado fraccionario. Por ejemplo: Si divido una pizza en dos partes, tengo dos mitades. Cada porción será 1/2 de la pizza (una parte de dos). En caso de tomar ambas porciones, volveré a tener la pizza entera (2/2= 1).
Los números racionales pueden ser sumados, restados, multiplicados o divididos (excepto por cero). El resultado de estas operaciones será siempre otro número racional. Como los números enteros pueden ser positivos o negativos, se aplica la Ley de Signos. La forma de concretar las operaciones variará de acuerdo a la existencia o ausencia de igual denominador en las fracciones.
Números Irracionales
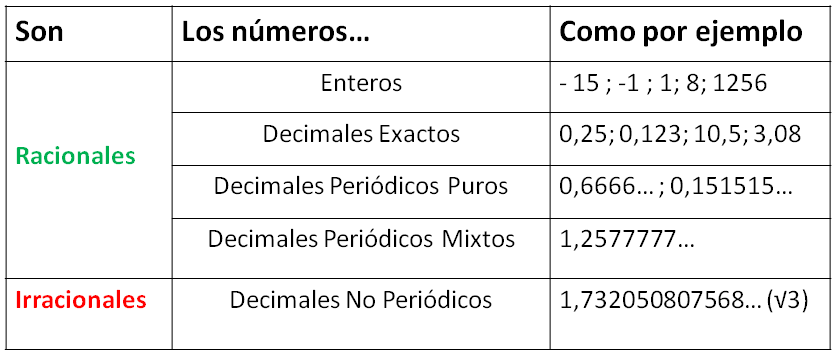
En matemáticas, un número irracional es un número que no puede ser expresado como una fracción m⁄n, donde m y n sean enteros y n sea diferente de cero. Es cualquier número real que no es racional, y su expresión decimal no es ni exacta ni periódica.
Un decimal infinito (es decir, con infinitas cifras) aperiódico, como √7 = 2,64575131106459059050161... no puede representar un número racional. A tales números se les nombra "números irracionales". Esta denominación significa la imposibilidad de representar dicho número como razón de dos números enteros. El número pi (), número e y el número áureo () son otros ejemplos de números irracionales.
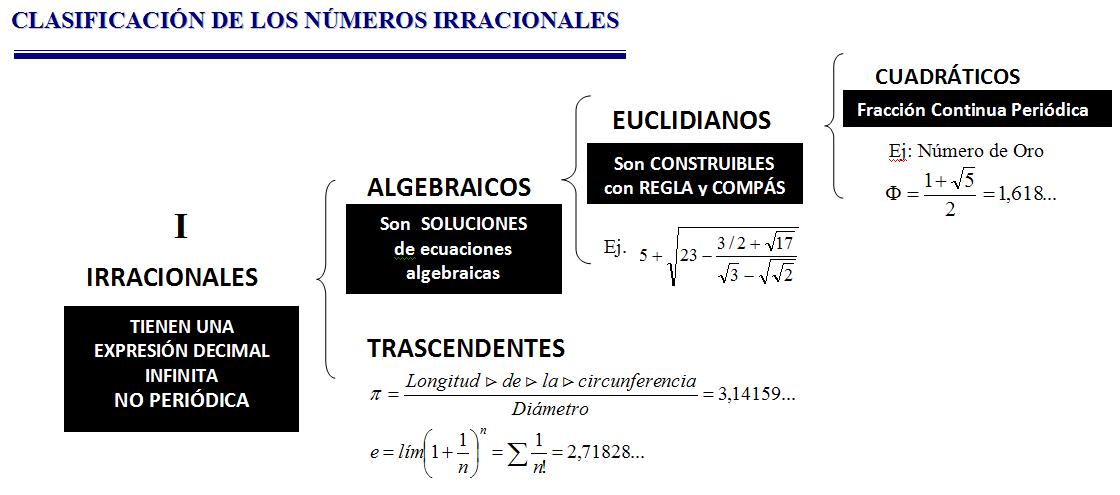
Clasificación de los números Irracionales

Numeros Reales
Los números reales son cualquier número que corresponda a un punto en la recta real y pueden clasificarse en números naturales, enteros, racionales e irracionales.
En otras palabras, cualquier número real está comprendido entre menos infinito y más infinito y podemos representarlo en la recta real.



No hay comentarios:
Publicar un comentario